The experience of the hot air balloon challenge is a good example of my notion of language sets as they pertain to knowledge, specifically, knowledge encapsulated in language. Easily identifiable language sets are the various spoken languages such as English, Spanish, French, Russian, Chinese and so on and so forth. As we have seen within the language set of English, there are also other self-defined language sets. When studying various disciplines in academia, one must come to terms with the jargon of the given field of study. The various jargons are themselves language sets particular to that field.
Mathematics is a language set. Within Mathematics (just as within English) there exist other self-defined language sets. As I have tried to indicate, there is a knowledge base encapsulated in, and is often times unique to, the given language set. Consider algebra as opposed to geometry as opposed to calculus.
To come to terms and gain an understanding of the limits of human knowledge, I believe Mathematics to be a most helpful language set for the task at hand. A simple way to perceive human knowledge in the context of the universe is to recall the number line and the language pertinent to graphing points in space.
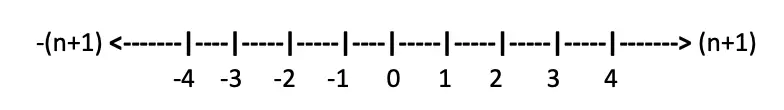
To any number, no matter how large, I can always add 1 [n+1]. Thus the natural number line is infinite in both the positive and the negative directions. The use of the word ‘directions’ is noteworthy. Positive (+) and negative (-) are terms of direction. They encapsulate a relative position (to the right or left) of the point of origin. They do not encapsulate magnitude (or quantity). The natural numbers (1, 2, 3, 4 … [n+1]) encapsulate magnitude. In any event, it is clear that the number line is infinitely long because it represents an infinite number of points. Thus there is an infinity of natural numbers, but there is also an infinity between each natural number.
For this description we will consider the space between 0 and 1. The mid-point between 0 and 1 is the ½. The mid-point between 0 and ½ is ¼. The mid-point between 0 and ¼ is 1/8. Continuation of this process demonstrates that just as the number line of natural numbers or counting numbers is infinitely large so is the space or points between 0 and 1 equally infinite. If one wished, one could argue that between any two points there exists an infinity of points. It would be a point well taken. However, to keep this process simple and manageable, suffice it to say that infinity exists between 0 and 1 and that this same quantified infinity exists between every other unit between natural numbers ( i.e. between 3 and 4; 65 and 66; 2×1010 and 2×1010+1). I can therefore refine my understanding of the infinity represented by the number line thusly:
Since the units between 0 and 1, 1 and 2 and so forth are infinite, the number line can be understood as an infinity of infinities.

Three dimensional space is defined by three number lines or axis which are traditionally represented by the letters x, y, and z. Thus, we have the following as being true:
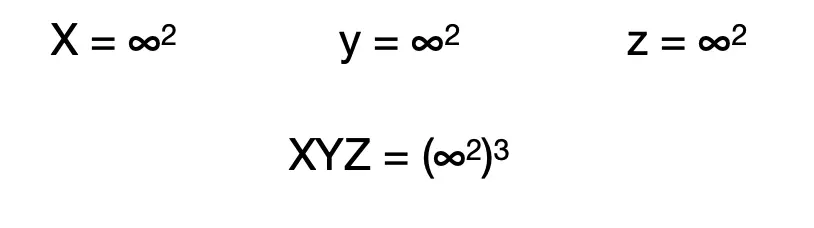
That is more infinity than infinity ( ∞ ). This understanding of the infinity of three dimensional space is a bit more precise than simply saying that space is infinite ( ∞ ) just like the use of the language set of navigation is more useful than the more generic terms of “up, down, left and right” for flying a computer simulated, hot air balloon.








Recalling the basic number line and expanding the knowledge it encapsulates into an understanding of the infinity of three dimensional space serves to build the foundation upon which to posit the following analogy, but before I make the analogy, I am mindful of Jacob Bronowski’s reflections upon Niels Bohr in The Ascent of Man (1973).
His [Bohr’s] taste for the arts ran to poetry. He said to Heisenberg, “When it comes to atoms, language can be used only as in poetry. The poet, too, is not nearly so concerned with describing facts as with creating images”. That is an unexpected thought: when it comes to atoms, language is not describing facts but creating images. …Once we have discovered that the atoms are not the ultimate building blocks of matter, we can only try to make models of how the building blocks link and act together. The models are meant to show, by analogy, how matter is built up. (Page 349.)
It is by analogy that I hope to make my next point clear. The critical point is focused upon the very word ‘point’ and the poetic technique of invoking the multi-leveled meanings encased in one word or phrase. There is the point on a number line and there is a point to be made in a presented point of view.
The analogy goes like this. As there is an infinity of points that describe three dimensional space(∞2)3; so, too, there is an infinity of points to know about The Universe.

I can hear the clamor of objections in my internal dialogue. At first appearance this analogy seems to be a gross oversimplification, a writer’s (poet’s) trick of words and structure; and while all analogies break down in the end as this one will too [Bronowski. The Ascent of Man. 1973] , let us first see where this line of thinking takes us before we scrap it altogether. If Knowledge = (∞2)3, then it is obviously clear that human knowledge will fall quite short of knowing all there is to know, but Science is humanity’s equalizer. Science, one might argue, seeks to describe the laws that govern three dimensional space and the actions which lie therein as opposed to painting a complete portrait in detail.
To be completely open and honest, there is a third equation that is hovering in my thoughts. That equation is formed from the thought that Space (three dimensional or otherwise) is, by itself, not as important as what that Space encapsulates. In this instance, the space of which I am speaking encapsulates The Universe with some qualifications. Since the element of time is not present here, I am speaking of The Universe in a static, unchanging, situation as if frozen in time. A static universe is less complicated than a dynamic universe, therefore we are dealing with a less intense knowledge base. The dynamic aspect of time will be added later. If Space houses The Universe, then the size of The Universe is the size of Space and it is my contention that The Universe in its entirety fills Space. The Universe defines Space as opposed to Space defining The Universe.
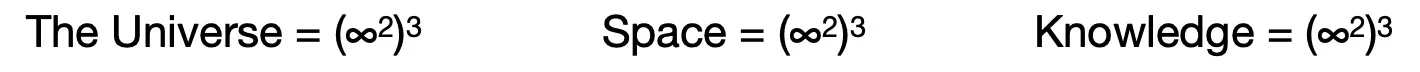
So, we are not taking about knowing Space. We are talking about knowing The Universe which is at least (∞2)3. To restate with substitution, Science, as humanity’s equalizer, seeks to describe the laws of The Universe. Given the magnitude of the problem [Knowledge = (∞2)3], Science, thus far, is the best that we can do. How good is our best?
A scientific law, if it is definitive, must account for every occurrence. Replication of the given experiments upon which the law is formulated must occur and the results must be identical. How many times must the law be tried and tested? History has shown that even long standing scientific beliefs are dropped as soon as one occurrence is found where the results did not hold up to the test. So, once the rigger of our scientific method has run its course long enough to accumulate enough trials and tests to establish a law, that law remains until someone finds an occurrence that breaks that law. Given the magnitude of reality, the magnitude of The Universe, (∞2)3; it is quite possible that human knowledge is unaware of those situations which render our science inaccurate. If it is possible that our science could be unaware of its errors, then how probable is it that our science is inaccurate? Some mathematics have been developed to calculate such probability. When writing up the results of an experiment, scientists will calculate the probable error present in his or her findings. The measure of a credibility level attached to a statistical analysis also attempts to account for human imperfection in assessing the matter at hand. What must be remembered, however, is that these calculations of probable error are not meant to warn the reader. On the contrary, these calculations are meant to instill high levels of certainty in the work being presented as true. Why would anyone want to know what is being presented if the authors were uncertain that they were expressing the truth? Quantum mechanics, however, as a scientific theory in physics, has, as one of its basic proponents, the principle of uncertainty. Loosely speaking, the principle of uncertainty defines what is known, but additionally defines what is not knowable.
If we add the dimension of Time and transform our static universe to a dynamic one, then we have an even more complicated and vast knowledge base to engage and conquer. James Gleick has some pertinent insights to offer in his book, Chaos, when considering our ability to know dynamic, closed systems, especially when considering The Universe as the ultimate closed, dynamic system. The first consideration is to ask the question: How robustly endowed with nonlinear elements is the full, accurate description of The Universe? If The Universe is replete with nonlinear elements or subsystems, then that knowledge base is less knowable because “Nonlinear systems generally cannot be solved and cannot be added together.” Consider Gleick’s following remarks:
Lorenz put the weather aside and looked for even simpler ways to produce this complex behavior [chaos]. He found one in a system of just three equations. They were nonlinear, meaning that they expressed relationships that were not strictly proportional. Linear relationships can be captured with a straight line on a graph. Linear relationships are easy to think about: the more the merrier. Linear equations are solvable, which makes them suitable for textbooks. Linear systems have an important modular virtue: you can take them apart, and put them together again – the pieces add up.
Nonlinear systems generally cannot be solved and cannot be added together. In fluid systems and mechanical systems, the nonlinear terms tend to be the features that people want to leave out when they try to get a good, simple understanding. Friction, for example. …nonlinearity means that the act of playing the game has a way of changing the rules. You cannot assign a constant importance to friction, because its importance depends on speed. Speed, in turn, depends on friction. The twisted changeability makes nonlinearity hard to calculate…analyzing the behavior of a nonlinear equation like the Navier-Stokes equation is like walking through a maze whose walls rearrange themselves with each step you take. (Pages 23, 24.)
Knowing a nonlinear system appears to be like knowing how to swim in the ocean. I know how to swim which means that I know how to travel through the water. This knowledge allows me to anticipate and, at times, allows me to catch a wave to body surf to shore. At other times I miss the timing and the wave washes over me. Just because I function thusly does not mean that I know the ocean in which I can swim. Just because we can navigate within a nonlinear system and perhaps describe its creative or chaotic side does not mean that we know that nonlinear system. Additionally, the statement, “Nonlinear systems generally cannot be solved and cannot be added together,” stands on its own merit regarding the inability to know. So, it appears that, as nonlinear elements or subsystems increase, the amount of knowable knowledge decreases.

Another component of chaos theory that is pertinent to the limits of human knowledge is the “sensitive dependence on initial conditions” that dynamic systems tend to demonstrate. The butterfly effect indicates that small input into dynamic systems lead to major output differences. If a nonlinear element or subsystem in The Universe runs its unpredictable course and adds even a small change to the dynamic of The Universe in its current state, then that small alteration can lead to major differences in the future course of The Universe.
It is time to recall the magnitude of the knowledge base of which we speak: Knowledge = (∞2)3. I do not have a magical number to answer the question: What percent of ‘What Is’ can be known by humans? Certainly, the knowledge base of the dynamic universe is far greater than that of a static universe. At this present moment I appeal not to the human mind, but to the human character (if the word ‘soul’ or the word ‘spirit’ conjures too much mysticism). What I hope can be felt or intuited, if you will allow, is, that, in spite of all of our medical, technological and scientific advances, when compared to the magnitude of The Universe, human knowledge is miniscule. Why is it important to have this perspective?
Oren Harman’s book, The Price of Altruism, serves as a good enough exhibit (there are many others, I am sure) to demonstrate the answer to the question of why it is important to know the limits of human knowledge regarding the laws of the Universe of which we, humans, are but tiny, tiny speck-like objects. In reading The Price of Altruism I traveled from Thomas Malthus, Charles Darwin and The Origin of Species and through a cadre of brilliant minds – Prince Peter Kropotkin, Thomas Henry Huxley, Warder Clyde Allee, Alfred Emerson, Vero Cope Wynne-Edwards, John von Neumann, B.F. Skinner, J.B.S. Haldane, William D. Hamilton and more — up to the death of George Price who was buried in an unmarked grave on January 22, 1975. The Price of Altruism is an award winning book, complete in itself and needs nothing other than to be read. At the risk of oversimplification, I observe that at the heart of the life that is this book is the human quest to resolve the human perceptions of reality as recorded by probing individuals beginning with the emergence of The Origin of Species. Using the death of George Price (1975) and the publication of The Origin of Species (1859) as parameters that define the generational discourse or argument, we experience the 116 year old quandary: Did humans evolve upon the principle of “survival of the fittest,” as creatures ascending to our current elevation upon the crushed corpses of the weaker versions of ourselves, or did humans evolve upon the principle of “mutual aid and mutual support,” as creatures who aid others at a possible cost to ourselves – ruthless competition or kind cooperation? George Price’s physical and mental condition at the time of his death aside, Harman observes on page 364 of a story that takes 365 pages to write:
He [Price] had been blessed with an unusual intelligence. He had seen things that the greatest minds had failed to see before him. And yet all his rational powers stood useless before the conundrum: It was impossible to know. …Despite the yearnings of his soul he was trapped in the prison of his brain. And, living in a squat with a broken window in the London winter, far away from his daughters, dejected, lonely, and weak, it may just have been a realization too difficult to bear.
The “realization too difficult to bear” was how could Price “discern if his selflessness was not just a masquerade, the self fooling the self only to please the self and nothing more?” The issue here is the ability to know, to know for sure, to know without any doubt whatsoever.
Harman observes on page 327 when discussing self-deception:
Which is it, then: pure genuine selflessness or an egoism so cunning that even the trickster is tricked? Some argue that the genuineness of goodness can be demonstrated scientifically, though their arguments seem really quite feeble. The strongest case that can be made for pure unsullied selflessness is that it is just as plausible as unadulterated egoism. Proponents call this “pluralism,” but in truth it is more of an admonition: There are questions that, however much we’d like to, science simply cannot solve.
Questions that science cannot solve turn my thinking once again to quantum mechanics. I understand quantum mechanics as parameters of possibilities governed by the principle of uncertainty. Discovering the exact position of an electron seems to be the recurring descriptive example used most often – the electron is somewhere in here (the electron cloud), but exactly where it is at any given time I could not tell you. Loosely, the electron cloud defines the territory (parameters of possibilities) of the electrons, but they (or it) could be anywhere within that cloud at any given time which is the principle of uncertainty. In a similar fashion, human knowledge has parameters governing the possibilities of what is knowable. Human knowledge cannot exist outside of those parameters. Human knowledge is therefore limited by those parameters. The language sets of science and mathematics are aspects, parts, possibilities of expression, and/or paths of thinking, that are part of the parameter matrix of human knowledge. There are other language sets in addition to those of science and mathematics. It is quite possible that certain types of human knowledge are better expressed with certain language sets and that each language set has its limitations of efficient function pertaining to expressing what is knowable for humans. It is noteworthy to see that The Price of Altruism is history, science, and biography spiced with a bit of economic theory, but the title . . . the title is . . . poetic.
Price, the man, and the ‘price’ he paid in his scientific quest as well as the economics of ‘price’ and value inherent in nature as the motivator of action are all present in the title. A single term pregnant with multiple levels of meaning is poetry not science. Science wants operant definitions that isolate one variable clearly defined from all other possibilities and then tests that variable’s actions and/or reactions. Poetry (Art) seeks the alternative to reductionism. Art seeks to build meaning to embrace complexity in all of its majesty in one intuitive moment of recognition (perhaps without full knowledge, but) with intangible understanding. If Harman’s observations are accurate, then Price paid the price for not accepting the limits of humanity’s scientific knowledge. Beyond being a personal lesson, this may be a cultural lesson as well. The poetry of The Price of Altruism moves me to assert that cultural self destruction is a likewise probable outcome of living as if (and/or needing to feel that) your point of view is absolute truth. I believe that there are absolutes in The Universe, but I do not believe that humans can know all (or perhaps even most) of them. Human knowledge is limited, has always been limited and will always be limited. Just as we cannot expect an ant to know more than an ant can know, so we cannot know more than a human can know. We should act accordingly.
